The #2020MathProject is centered around gaining clarity of the values of habits in relation to goals. In order to more accurately assess the value of your habits, you have to spend some time getting clear on your values and goals. What is the underlying why that motivates you to take action? I just finished rereading […]
Month: December 2019
Controlled Circles

Geometry lesson of the day: Concentric Circles consist of two or more circles that fit inside one another and share a center point but have different radius lengths. A target or bullseye is a common example of concentric circles, where attention is directed to the smallest circle surrounding the center. If you’ve read Stephen Covey’s […]
8 Days of Infinity

Infinity has no end. It is boundless, limitless. While infinity can be used like a real number, it does not behave like a real number; infinity is greater than any real number. It cannot be measured and does not grow; it is the opposite of finite. The infinity symbol ∞ is also known as the […]
Numero Uno
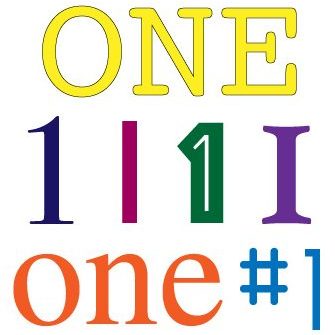
1 is the basic building block of our number system; a single identity; a unit. The first positive integer, 1 is neither prime nor composite. In mathematics, 1 is also the only number for which these facts are true (so says Wikipedia): Any number n multiplied by 1 equals that number: n × 1 = n, example 7 × 1 = 7. […]
Calculate the Year in Review

The idea of making New Year’s resolutions for 2020 is a conflicting one for me personally, as I have never been one to make them. I firmly believe that part of my dissatisfaction with my track record of achievements in life can be attributed to not setting enough clearly defined goals or outlining specific plans […]
Goals + Action = Success

Are goals the integral component in the formula for success? Are you familiar with statistics on New Year’s resolutions? It’s that time of year again where about 60% of people start thinking about changes they want to make, yet an astonishing 8% of individuals who make New Year’s resolutions actually follow through consistently and meet […]
What is Metaphoric Math?

Metaphor is defined as: a figure of speech in which a word or phrase literally denoting one kind of object or idea is used in place of another to suggest a likeness or analogy between them (as in drowning in money). broadly : figurative language. -Merriam Webster dictionary Math, in the case of this blog, will encompass a wide range of mathematics […]
Welcome to Metaphoric Math

It’s about to get geeky. Math is a polarizing subject. Most people either love or hate it. Those who struggle to grasp the concepts often swear they will never use math in everyday life, while math nerds make their case for its daily applications with chart and graphs and percentages and statistics. I fall somewhere […]

